 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
10. Misure di frequenza delle malattieOBIETTIVI:
perché è importante calcolare gli intervalli di confidenza quando si effettuano misure di frequenza di malattia in un campione
Come già illustrato nella precedente unità didattica, le misure più frequentemente utilizzate per stimare la frequenza di una malattia in una popolazione sono l'incidenza e la prevalenza.
Molto spesso, queste misure non vengono effettuate sull'intera popolazione di interesse, ma su un 
campione di numerosità più o meno elevata. Ciò significa che, una volta concluso lo studio, i dati ottenuti non sono utili soltanto a conoscere la frequenza di malattia nel campione (cosa che in genere interessa poco), bensì, con un processo di inferenza, a stimare la frequenza di quella malattia nell'intera popolazione.
L'intervallo di confidenza fornisce informazioni riguardo alla precisione dei valori ottenuti attraverso lo studio di un campione.
Ad esempio, un intervallo di confidenza 95% comprende un intervallo di valori che tiene conto della variabilità del campione, in modo tale che si può confidare - con un margine di certezza ragionevole (appunto il 95%) - che quell'intervallo contenga il valore vero dell'intera popolazione che non hai avuto modo di esaminare. Ovviamente, ciò è vero solo se nello studio non sono presenti errori sistematici.
L'intervallo di confidenza rappresenta un parametro di fondamentale importanza soprattutto negli studi epidemiologici in cui la variabilità del campione (molto spesso dovuta al fatto che il campione è piccolo) può rendere aleatoria l'interpretazione dei risultati.
Questo stesso concetto è già stato illustrato nella unità didattica riguardante l'errore standard, ma credo che valga la pena di sottolinearlo di nuovo qui.
Per i più curiosi, dirò che, per calcolare l'intervallo di confidenza, è necessario un modello di probabilità che tenga conto dei diversi possibili risultati di uno studio. Di tali modelli ne esistono, in statistica, molti tipi (ad es. basati sulla distribuzione binomiale o su quella di Poisson oppure su quella gaussiana). In genere, quando il numero di osservazioni è abbastanza ampio, si utilizza proprio quest'ultimo modello di distribuzione gaussiana (detta anche "normale"). Comunque, non lasciarti intimorire da questi argomenti statistici un po' tecnici: per fortuna il calcolo dell'intervallo di confidenza è, come vedrai, molto semplice.
Data una certa prevalenza P, l'intervallo di confidenza 95% si ottiene con il calcolo della formula qui sotto, dove il segno +/- permette il calcolo di due valori: il limite superiore dell'intervallo (che si ottiene utilizzando il «+») e il limite inferiore (che si ottiene utilizzando il «-»):
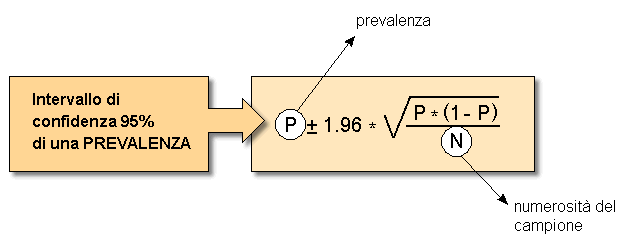
Analogamente, dato un certo valore di incidenza I, l'intervallo di confidenza 95% si ottiene nel modo seguente:
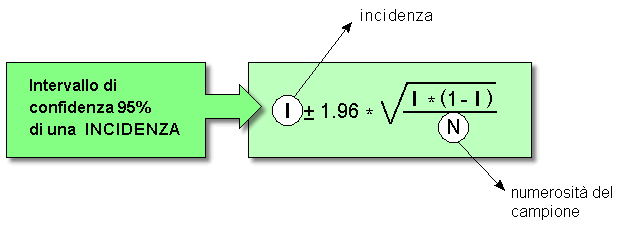
A questo punto. avrai di certo capito che la formula per il calcolo dell'intervallo di confidenza è una sorta di utilissimo «coltellino svizzero» che funziona in tutti i casi in cui hai calcolato una qualsiasi proporzione (o una percentuale):
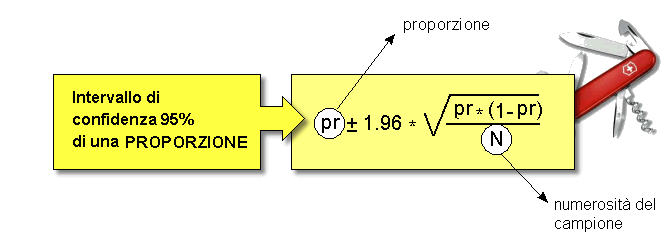
ESEMPIO. Supponiamo che in uno studio sulla 
displasia dell'anca di cani di razza "pastore tedesco" siano risultati affetti dalla malattia 18 cani su un campione di 180 cani esaminati. La prevalenza nel campione è: 18/180 = 0.1, cioè 10%.
Calcoliamo l'intervallo di confidenza 95%:
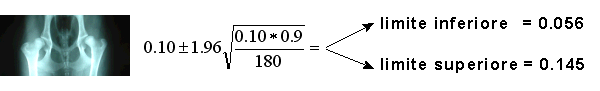
Pertanto, il limite inferiore dell'intervallo di confidenza 95% è 0.056 (5.6%) e il limite superiore 0.145 (14.5%). Ciò significa che, in media, il 95% di tali intervalli derivanti da studi privi di errori sistematici contiene il parametro vero della popolazione. In altre parole, possiamo essere abbastanza sicuri che la percentuale di cani con displasia dell'anca nella intera popolazione da cui è stato tratto il campione di 180 cani sia compresa fra 5.6 e 14.5%.
Infine, resta da ricordare che se vuoi ottenere un intervallo di confidenza 99% (invece che 95%), non devi far altro che sostituire il coefficiente 1.96 con 2.57.
ESEMPIO. Nello stesso studio sulla displasia dell'anca di cui sopra, calcolerai l'intervallo di confidenza 99% come segue:
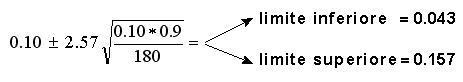
NELLA PROSSIMA UNITÀ:
si parla di una misura di frequenza (il tasso di attacco), che può essere considerata una particolare forma di incidenza, da utilizzare in determinate situazioni.
