 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
8. ProbabilitàOBIETTIVO:
definire il concetto di «probabilità» e calcolare la probabilità di eventi complessi
La maggior parte dei fenomeni che interessano la medicina è soggetta a variazioni casuali: ad esempio, il fattore di rischio (o «determinante») R può indurre la malattia M1 oppure la malattia M2 oppure nessuna malattia. Pertanto, è impossibile stabilire una relazione «se R allora M1»; bisogna invece affermare «se R, allora è probabile M1».
Il caso interviene in due tempi nelle osservazioni che si effettuano su una popolazione. Esso infatti dapprima è responsabile della variabilità fra gli individui (nessun individuo è uguale a nessun altro); in un secondo tempo, il caso agisce nuovamente quando si selezionano, per un determinato studio, alcune osservazioni dalla massa delle possibili osservazioni (cioè si esamina un 
campione).
Anche se l'effetto del caso si manifesta con una estrema complessità, il caso obbedisce tuttavia a leggi piuttosto semplici. La conoscenza di queste leggi pone il ricercatore in una condizione di superiorità rispetto all'osservatore empirico; in particolare, la conoscenza delle leggi del caso consente di valutare i fenomeni in base alla loro «probabilità».
Uno di punti di forza dell'epidemiologia è la capacità di fare previsioni. Per esempio, spesso si definisce il 
rischio relativo, cioè il rischio di contrarre malattia di animali con un determinato fattore (razza, o tipo di allevamento ecc.) rispetto al rischio corso da un gruppo di controllo non soggetto a quello stesso fattore. Più in generale, si può affermare che una delle più importanti attività di un epidemiologo è quella di calcolare la probabilità che si verifichi l'evento-malattia (o più in generale: un qualsiasi evento) in rapporto a particolari situazioni o fattori.
ESEMPI.
· È in corso una epidemia di una data malattia. Che probabilità c'è che un allevamento venga coinvolto?
· Un allevatore ha acquistato un animale proveniente da un allevamento in cui è presente una certa malattia. Che probabilità c'è che l'animale sia affetto da quella malattia?
· Stai trattando un gatto con una data terapia. Che probabilità c'è che il gatto guarisca? Che probabilità c'è che il gatto muoia?
· Una bovina è risultata positiva a un test per la diagnosi della tubercolosi. Che probabilità c'è che il test "dica la verità", ossia che quella bovina sia veramente ammalata?
· Un cane è affetto da displasia dell'anca. Che probabilità c'è che riacquisti la completa funzionalità dopo l'intervento operatorio?
La probabilità di un evento non è altro che l'espressione quantitativa della frequenza con cui esso si verifica.
Più propriamente, è bene parlare di «frequenza relativa»: infatti la probabilità (Pr) che si verifichi un evento aleatorio A è data dal rapporto tra il numero di casi favorevoli (quelli in cui A si verifica) e il numero di casi possibili (cioè il numero di volte che A può verificarsi). Da un punto di vista strettamente statistico, la probabilità viene definita come «la frequenza relativa di un evento, i cui valori sono compresi nell'intervallo [0;1] ove 0 indica un evento impossibile e 1 un evento certo.»
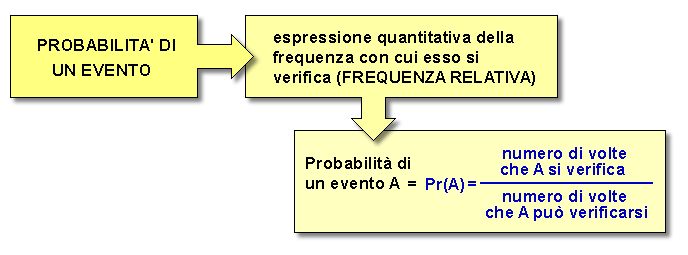
ESEMPIO 1. Lanciando una moneta l'evento «testa» si verifica una volta ogni due lanci, quindi la probabilità di tale evento è 1/2, cioè 0.5.
ESEMPIO 2. Qual è la probabilità che una carta da gioco estratta a caso da un mazzo di 52 sia un asso? Poiché nel mazzo vi sono 4 assi, la probabilità è di 4/52. In questo il numero di casi favorevoli è pari a 4 (asso di cuori, quadri, fiori, picche), mentre ognuna delle 52 carte del mazzo rappresenta un potenziale evento favorevole.
ESEMPIO 3. Supponiamo che in un episodio di avvelenamento da esteri fosforici in un allevamento di bovini si siano verificati 48 casi su un totale di 192 animali alimentati con il mangime contaminato. La probabilità di ammalare per un bovino scelto a caso è stata pertanto: 48/192 = 0.25 ovvero 25%.
Notare che, diversamente dai due esempi precedenti, in questo caso si tratta di una probabilità a posteriori, cioè valutata su un evento già accaduto.
Dagli esempi si nota che la probabilità può venire espressa attraverso una frazione, un numero decimale o una percentuale. Il numero decimale assume sempre un valore compreso fra 1 (quando l'evento si verifica sempre, e quindi il numeratore è uguale al denominatore) e 0 (quando l'evento non si verifica mai, e quindi il numeratore è uguale a 0).
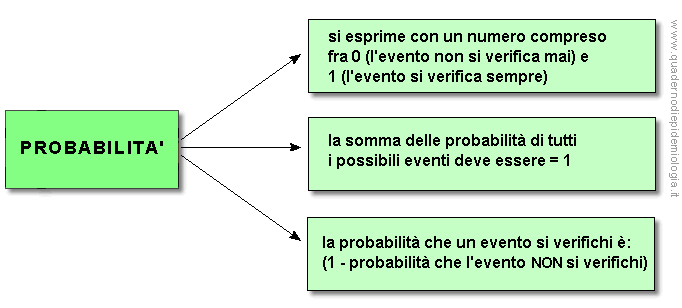
É intuitivo che:
Questo concetto ti sarà molto utile nel prossimo Capitolo, in cui imparerai le basi del Campionamento.
Ad esempio, se il 75% dei ceppi di Enterococcus è resistente alla tetraciclina, allora avremo una probabilità pari a 0.75 (75%) che un ceppo di Enterococcus preso a caso sia resistente.
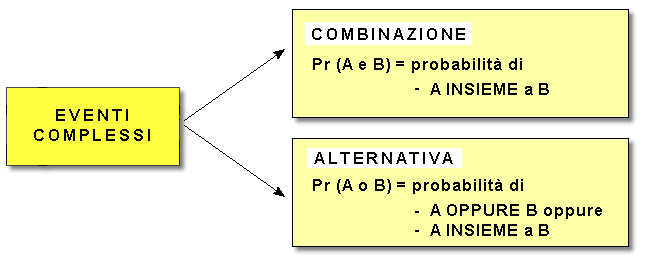
In alcuni casi è necessario calcolare la probabilità di eventi complessi, definiti come combinazioni specifiche (A e B) oppure alternative specifiche (A o B). Le regole che permettono di affrontare i più semplici problemi di probabilità di eventi complessi sono enunciate nella prossima unità.
Foglio di calcolo per Microsoft Excel® con una simulazione dei risultati (testa/croce) ottenibili lanciando una moneta.
AFTER HOURS: Splendido ornamento della ricerca umana
NELLA PROSSIMA UNITÀ:
si spiega ulteriormente la probabilità di eventi complessi, enunciando la «regola della addizione» e la «regola della moltiplicazione».
